Advertisements
Advertisements
प्रश्न
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
उत्तर
We have the following situation
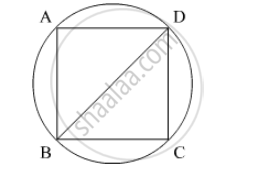
Let BD be the diameter and diagonal of the circle and the square respectively.
We know that area of the circle =`pir^2`
Area of the square = `"side"^2`
As we know that diagonal of the square is the diameter of the square.
Diagonal=`2r`
Side of the square= `"diagonal"/sqrt2............(1)`
Substituting "diagonal"=2r in equation (1) we get,
side of the square=`(2r)/sqrt2`
Now we will find the ratio of the areas of circle and square.
Area of circle/Area of square=`(pir^2)/((2r)/sqrt2)^2`
Now we will simplify the above equation as below,
Area of circle/Area of square=`(pir^2)/(r^2/2)`
Area of circle/Area of square=`pir^2xx2/(4r^2)`
Hence, `"Area of circle"/"Area of square"-pi/2`
Therefore, ratio of areas of circle and square is `pi:2`
APPEARS IN
संबंधित प्रश्न
A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
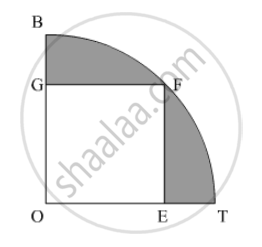
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
The area of the incircle of an equilateral triangle of side 42 cm is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
