Advertisements
Advertisements
प्रश्न
The area of the incircle of an equilateral triangle of side 42 cm is
विकल्प
\[22\sqrt{3} c m^2\]
231 cm2
462 cm2
924 cm2
उत्तर
Let ABC be the equilateral triangle such that AB = BC = CA = 42 cm. Also, let O be the centre and r be the radius of its incircle.
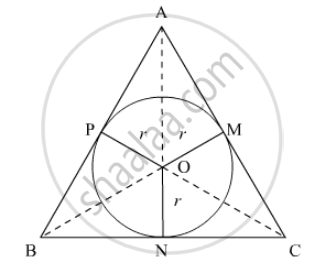
AB, BC and CA are tangents to the circle at M, N and P.
`∴ OM=ON=OP=r`
Area of ΔABC = Area (ΔOAB) + Area (ΔOBC) + Area (ΔOCA)
`⇒ sqrt3/4(42)^2=1/2xxrxxAB+1/2xxrxxBC+1/2xxrxx CA`
`⇒ sqrt3/4xx42xx42=1/2 r(AB+BC+CA)`
`⇒ 441sqrt3=1/2xxrxx(42+42+42)`
`⇒441sqrt3=1/2xxrxx(126)`
`⇒441sqrt3=63r`
`⇒r=(441sqrt3)/63`
`⇒ r=7sqrt3 cm`
Area of the circle `= pir^2=22/7 (7sqrt3)^2=22/7xx147=462 cm^2`
APPEARS IN
संबंधित प्रश्न
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
If the circumference of a circle increases from 4π to 8π, then its area is
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.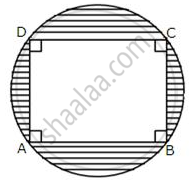
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
