Advertisements
Advertisements
प्रश्न
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.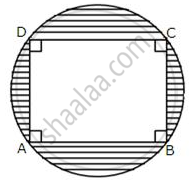
उत्तर
From the figure,
AB = 28 cm
BC = 21 cm
AC = `sqrt( "AB"^2 + "BC"^2 )`
= `sqrt( 28^2 + 21^2)`
= 35.
Hence diameter of the circle is 35 cm and hence
Area = π x `( 35/2 )^2` = 962.5 cm2
Area of the rectangle = 28 x 21 = 588 cm2
Hence area of the shaded portion is given by
A = 962 - 588 = 374.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
If diameter of a circle is increased by 40%, then its area increase by
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
The area of a sector whose perimeter is four times its radius r units, is
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
The circumference of a circular park is 352 m. Find the area of the park
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
