Advertisements
Advertisements
प्रश्न
The area of a sector whose perimeter is four times its radius r units, is
विकल्प
\[\frac{r^2}{4}\]
2r2 sq. units
r2 sq.units
उत्तर
We know that perimeter of the sector= `2r+θ/360xx2pir`
We have given that perimeter of the sector is four times the radius.
`2r+θ/360x2pir=4r`
Subtracting 2r from both sides of the equation,
`∴ θ/360xx2pir^=4r-2r`
`∴ θ/360xx2pir=2r`
Dividing both sides of the equation 2r we get,
`θ/360=pi=1`
`∴ θpi/360=1`.............(1)
Let us find the area of the sector.
∴ Area of the sector=`θ/360 pir^2`
Substituting `θpi/360=1` we get,
Area of the sector=`r^2`
Hence, area of the sector is `r^2 `sq.units
APPEARS IN
संबंधित प्रश्न
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The dimensions of a room are 14 m x 10 m x 6.5 m There are two doors and 4 windows in the room. Each door measures 2.5 m x 1.2 m and each window measures 1.5 m x 1 m. Find the cost of painting the four walls of the room at ₹ `35perm^2` .
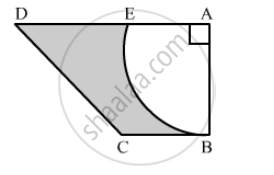
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

On decreasing the radius of a circle by 30%, its area is decreased by
The length of an arc of the sector of angle θ° of a circle with radius R is
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
