Advertisements
Advertisements
प्रश्न
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
उत्तर
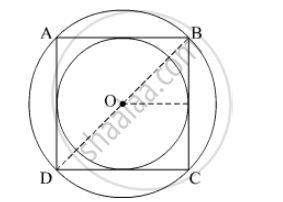
Let the side of the square inscribed in a square be a units.
Diameter of the circle outside the square = Diagonal of the square = \[\sqrt{2}a\]
Radius = \[\frac{\sqrt{2}a}{2} = \frac{a}{\sqrt{2}}\]
So, the area of the circle circumscribing the square =\[\pi \left( \frac{a}{\sqrt{2}} \right)^2\] .....(i)
Now, the radius of the circle inscribed in a square =\[\frac{a}{2}\]
Hence, area of the circle inscribed in a square = \[\pi \left( \frac{a}{2} \right)^2\] .....(ii)
From (i) and (ii)
\[ = \frac{\frac{1}{2}}{\frac{1}{4}}\]
\[ = \frac{2}{1}\]
Hence, the required ratio is 2 : 1.
APPEARS IN
संबंधित प्रश्न
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
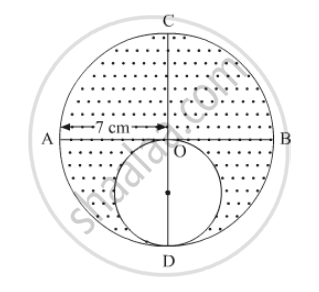
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
A sprinkler placed at the centre of a flower garden sprays water covering a circular area. If the area watered is 1386 cm2, find its radius and diameter
The area of the circle that can be inscribed in a square of side 6 cm is ______.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).