Advertisements
Advertisements
प्रश्न
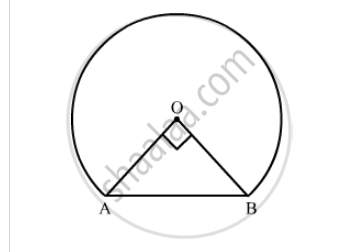
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
उत्तर
Let a be the side of square.
∴ Diameter of a circle = Diagonal of the square = 8 cm
In right angled triangle ABC,
Using Pythagoras theorem,
(AC)2 = (AB)2 + (BC)2
∴ (8)2 = a2 + a2
64 = 2a2
a2 = 32
Hence,
Area of square = a2
= 32 cm2
∴ Radius of the circle = `"Diameter"/2`
∴ Area of the circle = πr2
= π(4)2
= 16 cm2
Therefore, the area of the shaded region = Area of circle – Area of square
The area of the shaded region = 16π – 32
= `16 xx (22/7) - 32`
= `128/7`
= 18.286 cm2
APPEARS IN
संबंधित प्रश्न
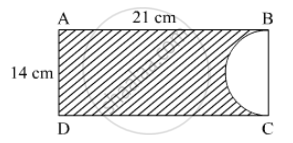
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
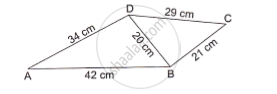
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
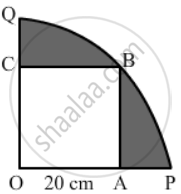
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is