Advertisements
Advertisements
प्रश्न
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
उत्तर
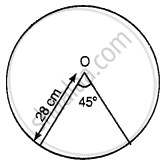
Given that, Radius of a circle, r = 28 cm
And measure of central angle θ = 45°
∴ Area of a sector of a circle = `(π"r"^2)/360^circ xx θ`
= `22/7 xx (28)^2/360^circ xx 45^circ`
= `(22 xx 28 xx 28)/7 xx 45^circ/360^circ`
= `22 xx 4 xx 28 xx 1/8`
= 22 × 14
= 308 cm2
Hence, the required area of a sector of a circle is 3082 cm.
APPEARS IN
संबंधित प्रश्न
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
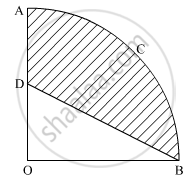
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
