Advertisements
Advertisements
प्रश्न
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
उत्तर
The statement is false because the area of a sector of a circle = `(1/2)"r"^2θ`, where r is the radius and θ the angle in radians subtended by the arc at the center of the circle.
It does not depend on the arc length.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
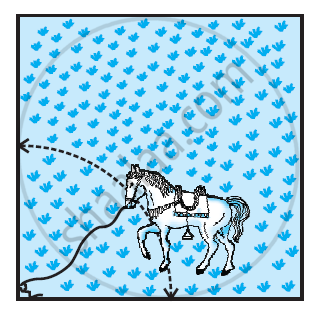
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
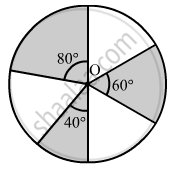
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).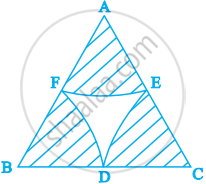
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
