Advertisements
Advertisements
प्रश्न
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
उत्तर
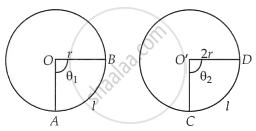
Let two circles C1 and C2 of radius r and 2r with centres O and O’, respectively.
It is given that, the arc length `hat("AB")` of C1 is equal to arc length `hat("CD")` of C2
i.e., `hat("AB") = hat("CD") = l` ...(say)
Now, let θ1 be the angle subtended by arc `hat("AB")` and θ2 be the angle subtended by arc `hat("CD")` at the centre.
∴ `hat("AB") = l = θ_1/360^circ xx 2π"r"` ...(i)
And `hat("CD") = l = θ_2/360^circ xx 2π (2"r")`
= `θ_2/360^circ xx 4π"r"` ...(ii)
From (i) and (ii), we get
`θ_1/360^circ xx 2π"r" = θ_2/360^circ xx 4π"r"`
⇒ θ1 = 2θ2
i.e., Angle of the corresponding sector of C1 is double the angle of the corresponding sector of C2.
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
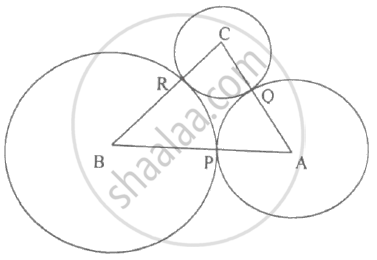
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
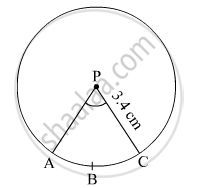
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
