Advertisements
Advertisements
Question
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Solution
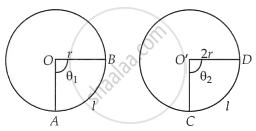
Let two circles C1 and C2 of radius r and 2r with centres O and O’, respectively.
It is given that, the arc length `hat("AB")` of C1 is equal to arc length `hat("CD")` of C2
i.e., `hat("AB") = hat("CD") = l` ...(say)
Now, let θ1 be the angle subtended by arc `hat("AB")` and θ2 be the angle subtended by arc `hat("CD")` at the centre.
∴ `hat("AB") = l = θ_1/360^circ xx 2π"r"` ...(i)
And `hat("CD") = l = θ_2/360^circ xx 2π (2"r")`
= `θ_2/360^circ xx 4π"r"` ...(ii)
From (i) and (ii), we get
`θ_1/360^circ xx 2π"r" = θ_2/360^circ xx 4π"r"`
⇒ θ1 = 2θ2
i.e., Angle of the corresponding sector of C1 is double the angle of the corresponding sector of C2.
APPEARS IN
RELATED QUESTIONS
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
(2) Area of any one of the sectors
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
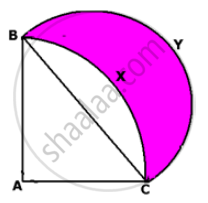
The area of the shaded portion in the following figure is equal to the area of.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
