Advertisements
Advertisements
Question
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
Options
`p/180 xx 2piR`
`p/180 xxpiR^2`
`p/360 xx 2piR`
`p/720 xx 2 pi R^2`
Solution
Area of a sector of angle p (in degrees) of a circle with radius R is `bbunderline(P/720 xx 2 pi R^2)`.
Explanation:

We know that area of sector of angle θ = `theta/360^@ xx piR^2`
Area of sector of angle P = `p/360^@(piR^2)`
`= theta/(360°) xx piR^2`
`= p/(360°) xx piR^2`
`= 2/2 xx (p/(360°) xx piR^2)`
Hence, `p/(720°) xx 2 pi R^2` is the correct answer.
APPEARS IN
RELATED QUESTIONS
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
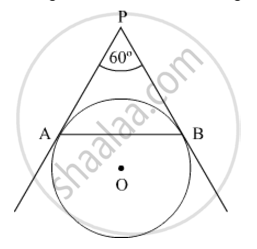
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
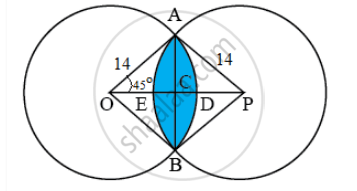
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
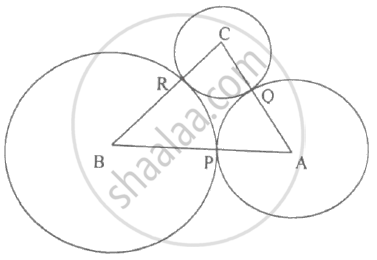
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.

Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
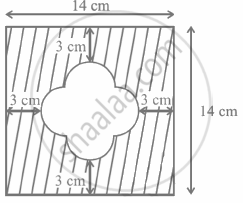
The area of the shaded portion in the following figure is equal to the area of.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.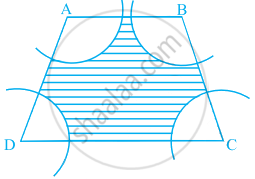
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
Find the area of the unshaded region shown in the given figure.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
