Advertisements
Advertisements
Question
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Solution
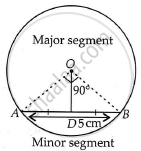
Let the radius of the circle be r.
Given that, length of chord of a circle, AB = 5 cm
And central angle of the sector AOBA (θ) = 90°
Now, in ΔAOB,
(AB)2 = (OA)2 + (OB)2 ...[By Pythagoras theorem]
(5)2 = r2 + r2
⇒ 2r2 = 25
∴ r = `5/sqrt(2) "cm"`
Now, in ΔAOB we draw a perpendicular line OD, which meets at D on AB and divides chord AB into two equal parts.
So, AD = DB
= `"AB"/2`
= `5/2 "cm"` ...[∵ The perpendicular drawn from the centre to the chord of a circle divides the chord into two equal parts]
By Pythagoras theorem, in ΔADO,
OA2 = OD2 + AD2
⇒ OD2 = OA2 – AD2
= `(5/sqrt(2))^2 - (5/2)^2`
= `25/2 - 25/4`
= `(50 - 25)/4`
= `25/4`
⇒ OD = `5/2 "cm"`
∴ Area of an isosceles ΔAOB
= `1/2 xx "AB" xx "OD"`
= `1/2 xx 5 xx 5/2`
= `25/4 "cm"^2`
Now, area of sector AOBA
= `(pi"r"^2)/360^circ xx θ`
= `(pi xx (5/sqrt(2))^2)/360^circ xx 90^circ`
= `(pi xx 25)/(2 xx 4)`
= `(25pi)/8 "cm"^2`
∴ Area of minor segment
= Area of sector AOBA – Area of an isosceles ΔAOB
= `((25pi)/8 - 25/4) "cm"^2`
Now, area of the circle
= πr2
= `pi(5/sqrt(2))^2`
= `(25pi)/2 "cm"^2`
∴ Area of major segment
= Area of circle – Area of minor segment
= `(25pi)/2 - ((25pi)/8 - 25/4)`
= `(25pi)/8 (4 - 1) + 25/4`
= `((75pi)/8 + 25/4) "cm"^2`
∴ Difference of the areas of two segments of a circle
= Area of major segment – Area of minor segment
= `((75pi)/8 + 25/4) - ((25pi)/8 - 25/4)`
= `((75pi)/8 - (25pi)/8) + (25/4 + 25/4)`
= `(75pi - 25pi)/8 + 50/4`
= `(50pi)/8 + 50/4`
= `((25pi)/4 + 25/2) "cm"^2`
Hence, the required difference of the areas of two segments is `((25pi)/4 + 25/2) "cm"^2`.
APPEARS IN
RELATED QUESTIONS
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector

In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.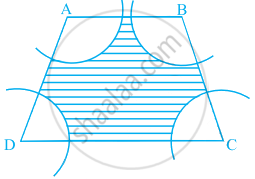
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
