Advertisements
Advertisements
Question
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
Solution
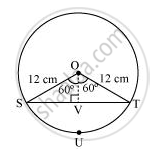
Let us draw a perpendicular OV on chord ST. It will bisect the chord ST.
SV = VT
In ΔOVS,
`(OV)/(OS) = cos 60º`
`(OV)/12 = 1/2`
OV = 6 cm
`(SV)/(SO) = sin 60^@ = sqrt3/2`
`(SV)/12 = sqrt3/2`
`SV = 6sqrt3 cm`
ST = 2SV
= `2xx6sqrt3`
= `12sqrt3 "cm"`
Area of ΔOST =` 1/2 xx ST xx OV`
`1/2xx12sqrt3xx6`
= `36sqrt3`
= 36 × 1.73
= 62.28 cm2
Area of sector OSUT = `120^@/360^@ xx pi(12)^2`
`=1/3xx3.14 xx 144 = 150.72 cm^2`
Area of segment SUT = Area of sector ΔSUT − Area of ΔOST
= 150.72 − 62.28
= 88.44 cm2
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
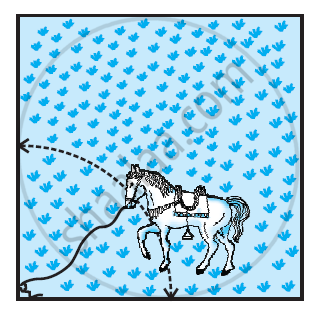
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.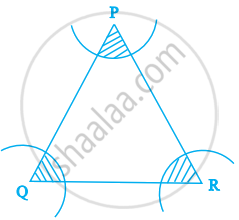
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
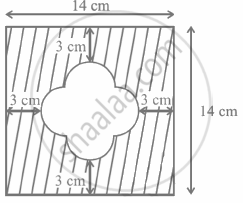
Find the area of the unshaded region shown in the given figure.