Advertisements
Advertisements
Question
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
Solution
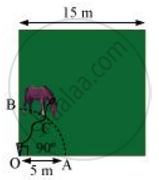
i) From the figure, it can be observed that the horse can graze a sector of 90° in a circle of 5 m radius.
Area that can be grazed by horse = Area of sector OACB
`= (90^@)/360^@ pir^2`
`=1/4xx 3.14xx (5)^2`
= 19.625 m2
ii) Area that can be grazed by the horse when length of rope is 10 m long
`=(90^@)/(360^@) xx pi xx (10)^2 `
=`1/4 xx 3.14 xx 100`
= 78.5 m2
Increase in grazing area = (78.5 − 19.625) m2
= 58.875 m2
APPEARS IN
RELATED QUESTIONS
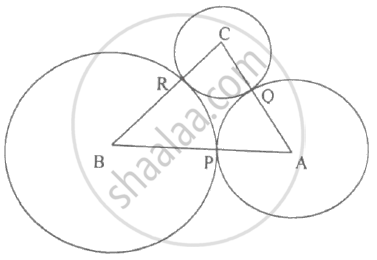
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
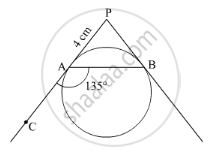
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
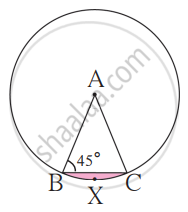
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Find the perimeter of a quadrant of a circle of radius 14 cm.
