Advertisements
Advertisements
Question
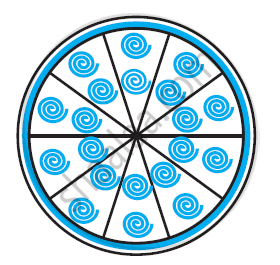
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
Solution
Total length of wire required will be the length of 5 diameters and the circumference of the brooch.
Radius of circle = `35/2` mm
Circumference of brooch = 2πr
`= 2 xx 22/7xx (35/2)`
= 110 mm
Length of wire required = 110 + 5 × 35
= 110 + 175 = 285 mm
It can be observed from the figure that each of 10 sectors of the circle is subtending 36° at the centre of the circle
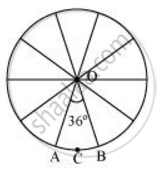
Therefore, area of each sector = `36^@/360^@ xx pir^2`
`=1/10xx22/7xx(35/2)xx(35/2)`
= `385/4` mm2
APPEARS IN
RELATED QUESTIONS
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
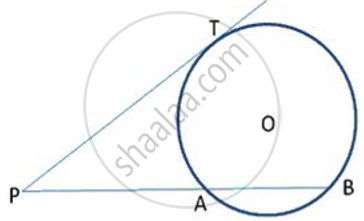
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The area of the shaded portion in the following figure is equal to the area of.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).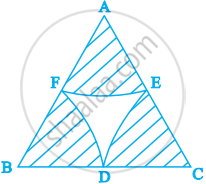
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.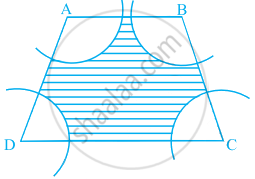
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
