Advertisements
Advertisements
Question
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
Solution
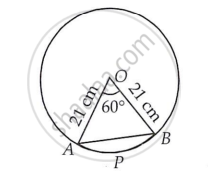
Area of the segment APB = [Area of the sector AOB] − [Area of ΔAOB] ....(1)
In AOB, OA = OB = 21 cm
∴ ∠A = ∠B = 60° ...(∴ ∠O = 60°)
AOB is an equilateral triangle.
∴ AB = 21 cm
∴ Area of ΔAOB = `sqrt3/4` (side)2 ....[∴ ΔAOB is an equilateral triangle]
`= sqrt3/4 xx 21 xx 21 "cm"^2`
= `(441sqrt3)/4` cm2 ...(2)
Using part (ii) and (2) in (1), we have
Area of the segment = `[231 "cm"^2] − [(441sqrt3)/4 "cm"^2]`
`= (231 - (441sqrt3)/4) "cm"^2`
RELATED QUESTIONS
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

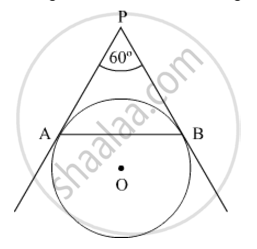
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
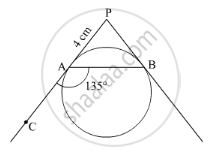
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
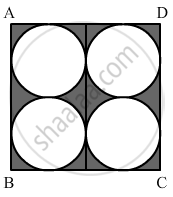
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
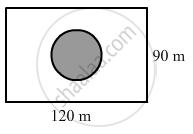
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
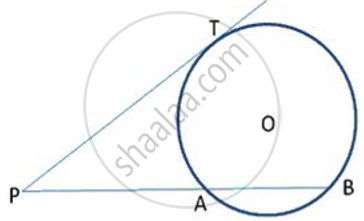
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The area of the shaded portion in the following figure is equal to the area of.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
