Advertisements
Advertisements
Question
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Solution
Given diameter of circle is d.
∴ Diagonal of inner square = Diameter of circle = d
Let side of inner square EFGH be x.
∴ In right angled ΔEFG,
EG2 = EF2 + FG2 ...[By Pythagoras theorem]
⇒ d2 = x2 + x2
⇒ d2 = 2x2
⇒ x2 = `"d"^2/2`
∴ Area of inner square EFGH = (Side)2
= x2
= `"d"^2/2`
But side of the outer square ABCD = Diameter of circle = d
∴ Area of outer square = d2
Hence, area of outer square is not equal to four times the area of the inner square.
APPEARS IN
RELATED QUESTIONS
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
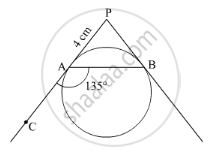
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).

A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
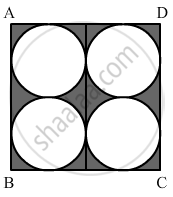
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
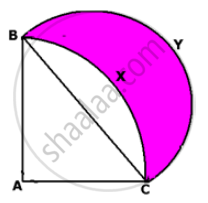
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the perimeter of a quadrant of a circle of radius 14 cm.
