Advertisements
Advertisements
प्रश्न
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
उत्तर
Given diameter of circle is d.
∴ Diagonal of inner square = Diameter of circle = d
Let side of inner square EFGH be x.
∴ In right angled ΔEFG,
EG2 = EF2 + FG2 ...[By Pythagoras theorem]
⇒ d2 = x2 + x2
⇒ d2 = 2x2
⇒ x2 = `"d"^2/2`
∴ Area of inner square EFGH = (Side)2
= x2
= `"d"^2/2`
But side of the outer square ABCD = Diameter of circle = d
∴ Area of outer square = d2
Hence, area of outer square is not equal to four times the area of the inner square.
APPEARS IN
संबंधित प्रश्न
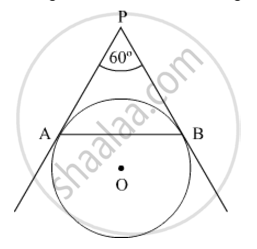
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
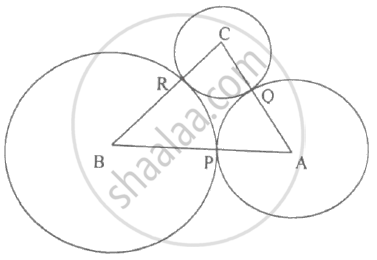
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
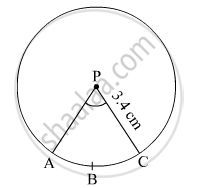
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
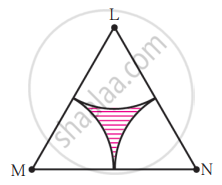
(2) Area of any one of the sectors
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).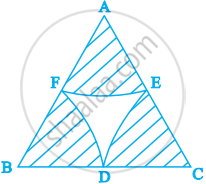
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
