Advertisements
Advertisements
प्रश्न
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
उत्तर
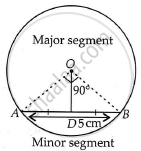
Let the radius of the circle be r.
Given that, length of chord of a circle, AB = 5 cm
And central angle of the sector AOBA (θ) = 90°
Now, in ΔAOB,
(AB)2 = (OA)2 + (OB)2 ...[By Pythagoras theorem]
(5)2 = r2 + r2
⇒ 2r2 = 25
∴ r = `5/sqrt(2) "cm"`
Now, in ΔAOB we draw a perpendicular line OD, which meets at D on AB and divides chord AB into two equal parts.
So, AD = DB
= `"AB"/2`
= `5/2 "cm"` ...[∵ The perpendicular drawn from the centre to the chord of a circle divides the chord into two equal parts]
By Pythagoras theorem, in ΔADO,
OA2 = OD2 + AD2
⇒ OD2 = OA2 – AD2
= `(5/sqrt(2))^2 - (5/2)^2`
= `25/2 - 25/4`
= `(50 - 25)/4`
= `25/4`
⇒ OD = `5/2 "cm"`
∴ Area of an isosceles ΔAOB
= `1/2 xx "AB" xx "OD"`
= `1/2 xx 5 xx 5/2`
= `25/4 "cm"^2`
Now, area of sector AOBA
= `(pi"r"^2)/360^circ xx θ`
= `(pi xx (5/sqrt(2))^2)/360^circ xx 90^circ`
= `(pi xx 25)/(2 xx 4)`
= `(25pi)/8 "cm"^2`
∴ Area of minor segment
= Area of sector AOBA – Area of an isosceles ΔAOB
= `((25pi)/8 - 25/4) "cm"^2`
Now, area of the circle
= πr2
= `pi(5/sqrt(2))^2`
= `(25pi)/2 "cm"^2`
∴ Area of major segment
= Area of circle – Area of minor segment
= `(25pi)/2 - ((25pi)/8 - 25/4)`
= `(25pi)/8 (4 - 1) + 25/4`
= `((75pi)/8 + 25/4) "cm"^2`
∴ Difference of the areas of two segments of a circle
= Area of major segment – Area of minor segment
= `((75pi)/8 + 25/4) - ((25pi)/8 - 25/4)`
= `((75pi)/8 - (25pi)/8) + (25/4 + 25/4)`
= `(75pi - 25pi)/8 + 50/4`
= `(50pi)/8 + 50/4`
= `((25pi)/4 + 25/2) "cm"^2`
Hence, the required difference of the areas of two segments is `((25pi)/4 + 25/2) "cm"^2`.
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
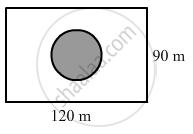
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
