Advertisements
Advertisements
प्रश्न
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
उत्तर
Angle subtended by sector at centre 𝜃 = 56°
Let radius be ‘x’ cm
Area of sector =`theta/360^@× pir^2`
=`56/360×22/7× r^2`
=`22/45`𝑟2
But area of sector = 4.4cm2 =`44/10cm^2`
`22/45r^2 =44/10`
⇒ `r^2 =(45×44)/(22×10)`= 9
⇒ 𝑟 = `sqrt(9)`
= 3 𝑐𝑚
∴ radius (r) = 3cm
APPEARS IN
संबंधित प्रश्न
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
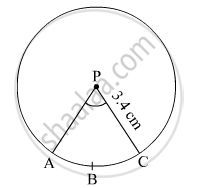
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
