Advertisements
Advertisements
प्रश्न
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
उत्तर
Given that,
Radius of circle = 7 cm
Central angle = 90°
Now, area of minor sector of circle
= `(πr^2θ)/360^circ`
= `(π(7)^2)/4`
= `(22 xx 7 xx 7)/(7 xx 4)`
= 38.5 cm2
Area of complete circle
= πr2
= π(7)2
= 154 cm2
Now, area of major sector
= Area of complete circle – Area of minor sector
= 154 – 38.5
= 115.5 cm2
APPEARS IN
संबंधित प्रश्न
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
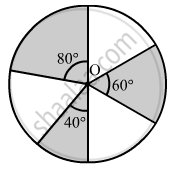
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
Find the perimeter of a quadrant of a circle of radius 14 cm.
