Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A chord of a circle subtends an angle ЁЭЬГ at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
рдЙрддреНрддрд░
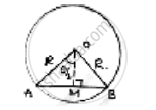
Let radius of circle = r
Area of circle = ЁЭЬЛЁЭСЯ2
AB is a chord, OA, OB are joined drop OM ⊥ AB. This OM bisects AB as well as ∠AOB.
∠AOM = ∠MOB =`1/2(0) =theta/2` AB = 2AM
In ΔAOM, ∠AMO = 90°
`"Sin"theta/2=(AM)/(AD)⇒ AM = R."sin"theta/2` AB = 2R sin`theta/2`
`"Cos"theta/2=(OM)/(AD)⇒ OM = R"cos"theta/2`
Area of segment cut off by AB = (area of sector) – (area of triangles)
=`theta/360× pir^2 −1/2`× ЁЭР┤ЁЭР╡ × ЁЭСВЁЭСА
`= r^2 [(pitheta)/360^@−1/2. 2"rsin"theta/2. R" cos"theta/2]`
`= R^2 [(pitheta)/360^@− "sin"theta/2. "cos"theta/2]`
Area of segment =`1/2`(ЁЭСОЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ЁЭСРЁЭСЦЁЭСЯЁЭСРЁЭСЩЁЭСТ)
`r^2 [(pitheta)/360− "sin"theta/2." cos"theta/2] =1/8pir^2`
`(8pitheta)/360^@− 8 "sin"theta/2. "cos"theta/2= pi`
`8 "sin"theta/2. "cos"theta/2+ pi =(pitheta)/45`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
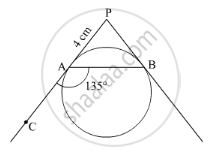
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
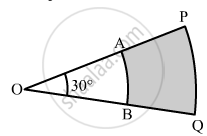
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
