Advertisements
Advertisements
प्रश्न
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
उत्तर
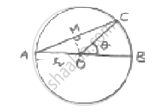
Given AB is diameter of circle with centre O
∠COB = 𝜃
Area of sector BOC =`theta/360^@× pir^2`
Area of segment cut off, by AC = (area of sector) – (area of ΔAOC)
∠AOC = 180 – 𝜃 [∠AOC and ∠BOC form linear pair]
Area of sector =`(180−theta)/360^@× pir^2 = (pir^2)/2−(pithetar)^2/360^@`
In ΔAOC, drop a perpendicular AM, this bisects ∠AOC and side AC.
Now, In ΔAMO, sin∠AOM =`(AM)/(DA)⇒ sin ((180−theta)/2) =(AM)/R`
⇒ AM = R sin(90 −`theta/2`) = 𝑅. cos`theta/2`
cos ∠ADM =`(OM)/(OA)⇒ cos (90 −theta/2) =(OM)/Y⇒ OM = R. "sin"theta/2`
Area of segment =`(pir^2)/2−(pithetar^2)/360^@−1/2`(𝐴𝐶 × 𝑂𝑀) [𝐴𝐶 = 2 𝐴𝑀]
`=(pir^2)/2−(pithetar^2)/360^@−1/2× (2 R "cos"theta/2R "sin"theta/2)`
`= r^2 [pi/2−(pitheta)/360^@−"cos"theta/2"sin"theta/2]`
Area of segment by AC = 2 (Area of sector BDC)`
`r^2[pi/2−(pitheta)/360^@− "cos"theta/2." sin"theta/2] = 2r^2 [(pitheta)/360^@]`
`"cos"theta/2." sin"theta/2=pi/2−(pitheta)/360−(2pitheta)/360^@`
`=pi/2−(pitheta)/360^@[1 + 2]`
`=pi/2−(pitheta)/360^@= pi(1/2−theta/120^@)`
`"cos"theta/2. "sin"theta/2= pi (1/2−theta/120^@)`
APPEARS IN
संबंधित प्रश्न
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
The area of the shaded portion in the following figure is equal to the area of.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Find the perimeter of a quadrant of a circle of radius 14 cm.
