Advertisements
Advertisements
प्रश्न
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
उत्तर
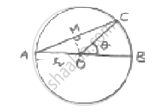
Given AB is diameter of circle with centre O
∠COB = 𝜃
Area of sector BOC =`theta/360^@× pir^2`
Area of segment cut off, by AC = (area of sector) – (area of ΔAOC)
∠AOC = 180 – 𝜃 [∠AOC and ∠BOC form linear pair]
Area of sector =`(180−theta)/360^@× pir^2 = (pir^2)/2−(pithetar)^2/360^@`
In ΔAOC, drop a perpendicular AM, this bisects ∠AOC and side AC.
Now, In ΔAMO, sin∠AOM =`(AM)/(DA)⇒ sin ((180−theta)/2) =(AM)/R`
⇒ AM = R sin(90 −`theta/2`) = 𝑅. cos`theta/2`
cos ∠ADM =`(OM)/(OA)⇒ cos (90 −theta/2) =(OM)/Y⇒ OM = R. "sin"theta/2`
Area of segment =`(pir^2)/2−(pithetar^2)/360^@−1/2`(𝐴𝐶 × 𝑂𝑀) [𝐴𝐶 = 2 𝐴𝑀]
`=(pir^2)/2−(pithetar^2)/360^@−1/2× (2 R "cos"theta/2R "sin"theta/2)`
`= r^2 [pi/2−(pitheta)/360^@−"cos"theta/2"sin"theta/2]`
Area of segment by AC = 2 (Area of sector BDC)`
`r^2[pi/2−(pitheta)/360^@− "cos"theta/2." sin"theta/2] = 2r^2 [(pitheta)/360^@]`
`"cos"theta/2." sin"theta/2=pi/2−(pitheta)/360−(2pitheta)/360^@`
`=pi/2−(pitheta)/360^@[1 + 2]`
`=pi/2−(pitheta)/360^@= pi(1/2−theta/120^@)`
`"cos"theta/2. "sin"theta/2= pi (1/2−theta/120^@)`
APPEARS IN
संबंधित प्रश्न
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

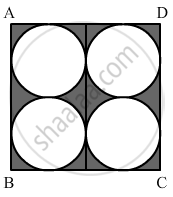
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
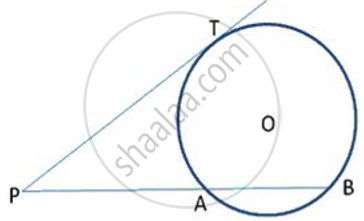
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
