Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
उत्तर
We know area of minor segment of the circle is \[A = \left\{ \frac{\pi\theta}{360} - \sin\frac{\theta}{2}\cos\frac{\theta}{2} \right\} r^2\]
\[\Rightarrow A = \left\{ \frac{\pi \times 90°}{360} - \sin\frac{90}{2}\cos\frac{90}{2} \right\} \left( 20 \right)^2 \]
\[ \Rightarrow A = \left( \frac{\pi}{4} - \frac{1}{2} \right)\left( 400 \right)\]
Area of the major segment = Area of the circle − area of the minor segment
\[= \pi \left( 20 \right)^2 - \left( 400 \right)\left[ \frac{\pi}{2} - \frac{1}{2} \right]\]
\[ = \left( 400 \right)\left[ \pi - \frac{\pi}{2} + \frac{1}{2} \right]\]
\[ = 1142 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
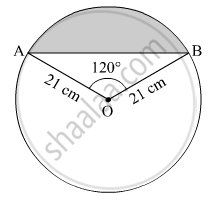
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
The circumference of a circular table is 88 m. Find its area.
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
