Advertisements
Advertisements
प्रश्न
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
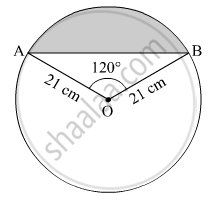
उत्तर
Construction: Draw a line passing through O and perpendicular to AB.
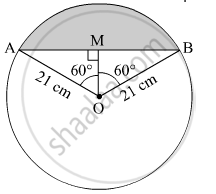
In ΔAOM and ΔBOM,
∠AMO = ∠BMO (by construction)
AO = BO (radius of the same circle)
OM = OM ( common side)
∴ ΔAOM ≅ Δ BOM (By RHS congruence rule)
We have , ∠AMO = ∠BMO = 60° (By CPCT) ....(i)
AM = BM (By CPCT) .......(ii)
In ΔAOM,
sin 60° = `"AM"/"OA" = "AM"/(21)`
⇒ `"AM"/(21) = sqrt3/(2)`
⇒ AM = `(21sqrt3)/(2) "cm"`
Also, cos 60° = `"OM"/"OA"`
⇒ `"OM"/"OA" = (1)/(2)`
⇒ `"OM"/"OA" = (21)/(2) "cm"`
AB = AM + MB = 2AM = `21sqrt3 "cm"` .......[from (ii)]
Area of sector AOB = `(120)/(360) · πr^2 = (1)/(3)· (22)/(7)· 21^2 = 462"cm"^2`
Area of ΔAOB = `(1)/(2) xx "OM" xx "AB" = (1)/(2) xx (21)/(2) xx 21 sqrt3 = (444sqrt3)/(4) "cm"^2 ≈ 191 "cm"^2`
Required area of segment = Area of sector AOB -">− Area of ΔAOB
= 462 - 191 = 271 cm2 (approx.)
APPEARS IN
संबंधित प्रश्न
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
The area of a sector whose perimeter is four times its radius r units, is
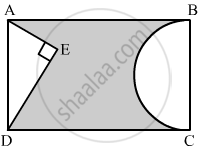
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
If the radius of a circle is tripled, the area becomes ______.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
