Advertisements
Advertisements
प्रश्न
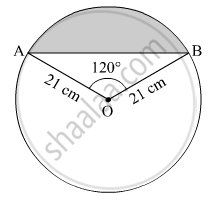
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
उत्तर
Construction: Draw a line passing through O and perpendicular to AB.
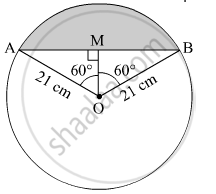
In ΔAOM and ΔBOM,
∠AMO = ∠BMO (by construction)
AO = BO (radius of the same circle)
OM = OM ( common side)
∴ ΔAOM ≅ Δ BOM (By RHS congruence rule)
We have , ∠AMO = ∠BMO = 60° (By CPCT) ....(i)
AM = BM (By CPCT) .......(ii)
In ΔAOM,
sin 60° = `"AM"/"OA" = "AM"/(21)`
⇒ `"AM"/(21) = sqrt3/(2)`
⇒ AM = `(21sqrt3)/(2) "cm"`
Also, cos 60° = `"OM"/"OA"`
⇒ `"OM"/"OA" = (1)/(2)`
⇒ `"OM"/"OA" = (21)/(2) "cm"`
AB = AM + MB = 2AM = `21sqrt3 "cm"` .......[from (ii)]
Area of sector AOB = `(120)/(360) · πr^2 = (1)/(3)· (22)/(7)· 21^2 = 462"cm"^2`
Area of ΔAOB = `(1)/(2) xx "OM" xx "AB" = (1)/(2) xx (21)/(2) xx 21 sqrt3 = (444sqrt3)/(4) "cm"^2 ≈ 191 "cm"^2`
Required area of segment = Area of sector AOB -">− Area of ΔAOB
= 462 - 191 = 271 cm2 (approx.)
APPEARS IN
संबंधित प्रश्न
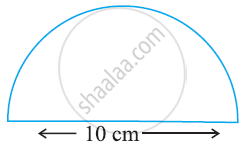
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
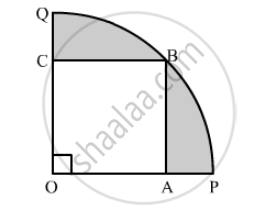
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

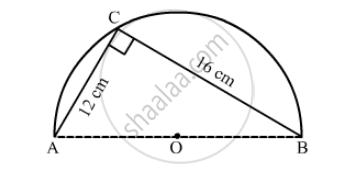
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
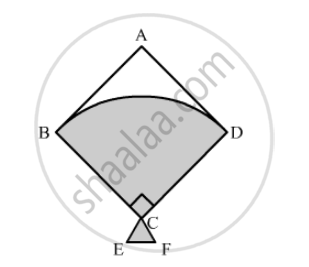
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Calculate the area of the shotput circle whose radius is 2.135 m.
