Advertisements
Advertisements
Question
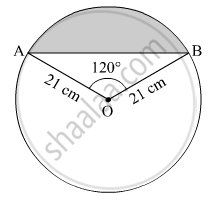
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Solution
Construction: Draw a line passing through O and perpendicular to AB.
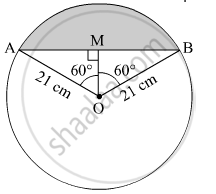
In ΔAOM and ΔBOM,
∠AMO = ∠BMO (by construction)
AO = BO (radius of the same circle)
OM = OM ( common side)
∴ ΔAOM ≅ Δ BOM (By RHS congruence rule)
We have , ∠AMO = ∠BMO = 60° (By CPCT) ....(i)
AM = BM (By CPCT) .......(ii)
In ΔAOM,
sin 60° = `"AM"/"OA" = "AM"/(21)`
⇒ `"AM"/(21) = sqrt3/(2)`
⇒ AM = `(21sqrt3)/(2) "cm"`
Also, cos 60° = `"OM"/"OA"`
⇒ `"OM"/"OA" = (1)/(2)`
⇒ `"OM"/"OA" = (21)/(2) "cm"`
AB = AM + MB = 2AM = `21sqrt3 "cm"` .......[from (ii)]
Area of sector AOB = `(120)/(360) · πr^2 = (1)/(3)· (22)/(7)· 21^2 = 462"cm"^2`
Area of ΔAOB = `(1)/(2) xx "OM" xx "AB" = (1)/(2) xx (21)/(2) xx 21 sqrt3 = (444sqrt3)/(4) "cm"^2 ≈ 191 "cm"^2`
Required area of segment = Area of sector AOB -">− Area of ΔAOB
= 462 - 191 = 271 cm2 (approx.)
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
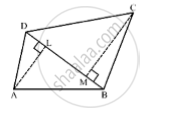
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
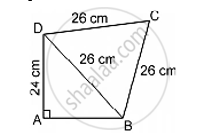
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
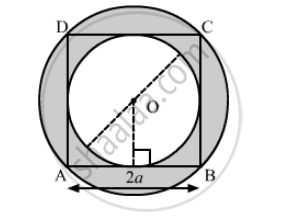
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
If the area of the circle is numerically equal to twice its circumference then what is the diameter of the circle?
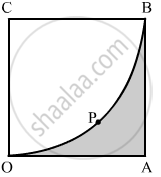
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
