Advertisements
Advertisements
Question
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
Options
2r
r2
r
\[\sqrt{r}\]
Solution
The triangle with the largest area will be symmetrical as shown in the figure.
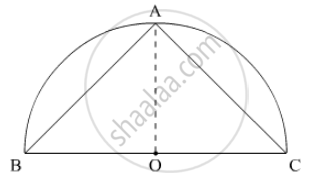
Let the radius of the circle be r.
Hence,
`ar (ΔABC)=1/2 (r)(2r)`
`= r^2"sq.unit"`
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
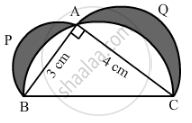
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
The ratio of the area of a circle to the area of its semicircle is
