Advertisements
Advertisements
प्रश्न
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

उत्तर
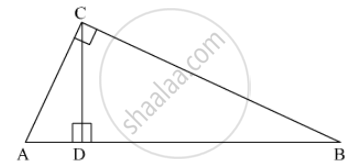
Given that :
CD ⊥ AB
∠ACB = 90°
To Prove : CD2 = BD x AD
Using Pythagoras Theorem in ΔACD
AC2 = AD2 + CD2 ....(1)
Using Pythagoras Theorem in ΔCDB
CB2 = BD2 + CD2 ....(2)
Similarly in ΔABC,
AB2 = AC2 + BC2 ....(3)
As AB = AD + DB
⇒AB = AD + BD ....(4)
Squaring both sides of equation (4), we get
(AB)2 = (AD+BD)2
⇒AB2 = AD2 + BD2 + 2 x BD x AD
From equation (3) we get
⇒ AC2 + BC2 = AD2 + BD2 + 2 x BD x AD
Substituting the value of AC2 from equation (1) and the value of BC2 from eqution (2), we get
AD2 + CD2 + BD2 + CD2 = AD2 + BD2 + 2 x BD x AD
⇒ 2 CD2 = 2 x BD x AD
⇒ CD2 = BD x AD
Hence Proved.
संबंधित प्रश्न
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Find the unknown side in the following triangles
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

