Question

In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD² = BD x AD.

Answer 1

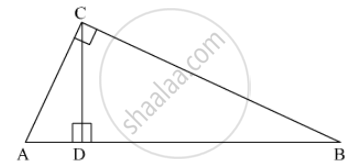
Given that :
CD ⊥ AB
∠ACB = 90°

To Prove : CD² = BD x AD
Using Pythagoras Theorem in ΔACD
AC² = AD² + CD²                                  ....(1)

Using Pythagoras Theorem in ΔCDB
CB² = BD² + CD²                                   ....(2)

Similarly in ΔABC,
AB² = AC² + BC²                                    ....(3)

As AB = AD + DB
⇒AB = AD + BD                                     ....(4) 

Squaring both sides of equation (4), we get
(AB)² = (AD+BD)²
⇒AB² = AD² + BD² + 2 x BD x AD

From equation (3) we get 
⇒ AC² + BC² = AD² + BD² + 2 x BD x AD

Substituting the value of AC² from equation (1) and the value of BC² from eqution (2), we get
AD² + CD² + BD² + CD² = AD² + BD² + 2 x BD x AD
⇒ 2 CD² = 2 x BD x AD
⇒ CD² = BD x AD
Hence Proved.