Advertisements
Advertisements
प्रश्न
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

उत्तर
Given :
∆ ACD = ∠ABC = 90°
and AD = 13 cm, BC = 12 cm, AB = 3 cm
To find : Length of DC.
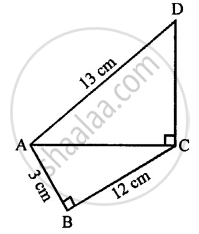
(i) In right angled ∆ ABC
AB = 3 cm, BC = 12 cm
According to Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
(AC)2 = (3)2 + (12)2
(AC) =`sqrt(9+144)=sqrt153` cm
(ii) In right angled ∆ ACD
AD = 13 cm, AC =`sqrt153`
According to Pythagoras Theorem,
DC2 = AB2 − AC2
DC2= 169 − 153
DC = `sqrt16` = 4 cm
∴ Length of DC is 4 cm
APPEARS IN
संबंधित प्रश्न
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
Two angles are said to be ______, if they have equal measures.
