Advertisements
Advertisements
Question
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Solution
Given :
∆ ACD = ∠ABC = 90°
and AD = 13 cm, BC = 12 cm, AB = 3 cm
To find : Length of DC.
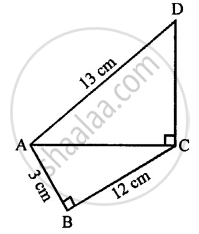
(i) In right angled ∆ ABC
AB = 3 cm, BC = 12 cm
According to Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
(AC)2 = (3)2 + (12)2
(AC) =`sqrt(9+144)=sqrt153` cm
(ii) In right angled ∆ ACD
AD = 13 cm, AC =`sqrt153`
According to Pythagoras Theorem,
DC2 = AB2 − AC2
DC2= 169 − 153
DC = `sqrt16` = 4 cm
∴ Length of DC is 4 cm
APPEARS IN
RELATED QUESTIONS
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
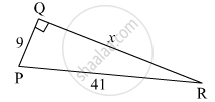
In the figure below, find the value of 'x'.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two squares are congruent, if they have same ______.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
