Question

If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.

Options

• PR . QR = RS²

• QS² + RS² = QR²

• PR² + QR² = PQ²

• PS² + RS² = PR²

Answer 1

If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then PR² + QR² = PQ².

Explanation:

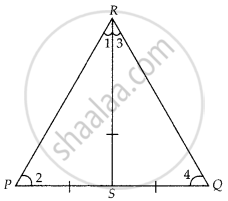
Given, in ∆PQR,

PS = QS = RS  ...(i)

In ∆PSR,

PS = RS  ...[From equation (i)]

⇒ ∠1 = ∠2  ...(ii) [Angles opposite to equal sides are equal]

Similarly, in ∆RSQ,

RS = SQ

⇒ ∠3 = ∠4  ...(iii) [Angles opposite to equal sides are equal]

Now, in ∆PQR,

Sum of angles = 180°

⇒ ∠P + ∠Q + ∠P = 180°

⇒ ∠2 + ∠4 + ∠1 + ∠3 = 180°

⇒ ∠1 + ∠3 + ∠1 + ∠3 = 180°

⇒ 2(∠1 + ∠3) = 180°

⇒ ∠1 + ∠3 = `180^circ/2` = 90°

∴ ∠R = 90°

In ∆PQR, by Pythagoras theorem,

PR² + QR² = PQ²