Advertisements
Advertisements
Question
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
Solution
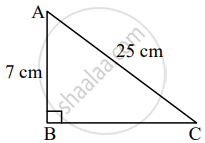
Let ∆ABC be the given right angled triangle.
AC = 25 cm, AB = 7 cm
In ∆ABC, ∠B = 90° ......[Given]
∴ AC2 = AB2 + BC2 .......[Pythagoras theorem]
∴ 252 = 72 + BC2
∴ 625 = 49 + BC2
∴ BC2 = 625 – 49
∴ BC2 = 576
∴ BC = 24 cm .......[Taking square root of both sides]
∴ The length of the base of the given right angle triangle is 24 cm.
APPEARS IN
RELATED QUESTIONS
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two circles having same circumference are congruent.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
