Advertisements
Advertisements
प्रश्न
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
उत्तर
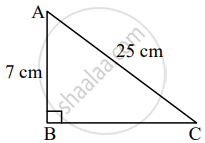
Let ∆ABC be the given right angled triangle.
AC = 25 cm, AB = 7 cm
In ∆ABC, ∠B = 90° ......[Given]
∴ AC2 = AB2 + BC2 .......[Pythagoras theorem]
∴ 252 = 72 + BC2
∴ 625 = 49 + BC2
∴ BC2 = 625 – 49
∴ BC2 = 576
∴ BC = 24 cm .......[Taking square root of both sides]
∴ The length of the base of the given right angle triangle is 24 cm.
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
Find the Pythagorean triplet from among the following set of numbers.
9, 40, 41
In a right angled triangle, the hypotenuse is the greatest side
In the figure, find AR
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
The longest side of a right angled triangle is called its ______.
Two squares are congruent, if they have same ______.
