Advertisements
Advertisements
प्रश्न
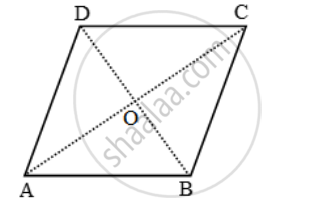
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
उत्तर १
Let the diagonals AC and BD of rhombus ABCD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90º and AO = CO, BO = OD.
Since ∆AOB is a right triangle right-angle at O.
∴ AB2 = OA2 + OB2
`AB^2=(1/2AC)^2 +(1/2BD)^2 `
⇒ 4AB2 = AC2 + BD2 ….(i)
Similarly, we have
`4BC^2 = AC^2 + BD^2 ….(ii)`
`4CD^2 = AC^2 + BD^2 ….(iii)`
and,
`4AD^2 = AC^2 + BD^2 ….(iv)`
Adding all these results, we get
`4(AB^2 + BC^2 + AD^2 ) = 4(AC^2 + BD^2 )`
`⇒ AB^2 + BC^2 + AD^2 + DA^2 = AC^2 + BD^2`
उत्तर २

In ΔAOB, ΔBOC, ΔCOD, ΔAOD
Applying Pythagoras theorem
AB2 = AO2 + OB2
BC2 = BO2 + OC2
CD2 = CO2 + OD2
AD2 = AO2 + OD2
Adding all these equations,
AB2 + BC2 + CD2 + AD2
= 2(AO2 + OB2 + OC2 + OD2)
= `2{("AC"/2)^2 + ("BD"/2)^2 + ("AC"/2)^2 + ("BD"/2)^2}` ...(diagonals bisect each other)
= `2(("AC")^2/2 + ("BD")^2/2)`
= (AC)2 + (BD)2
APPEARS IN
संबंधित प्रश्न
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
Two angles are said to be ______, if they have equal measures.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
