Advertisements
Advertisements
प्रश्न
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
उत्तर
In the triplet (3, 5, 4),
32 = 9, 52 = 25, 42 = 16 and 9 + 16 = 25
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (3, 5, 4) is a pythagorean triplet.
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the figure below, find the value of 'x'.
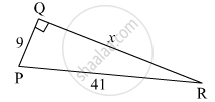
In the figure below, find the value of 'x'.

In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
In the figure, find AR
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
