Advertisements
Advertisements
प्रश्न
In the figure below, find the value of 'x'.

उत्तर
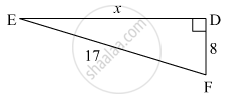
In the right-angled triangle EDF,
∠D = 90°.
Hence, side EF is the hypotenuse.
According to Pythagoras' theorem,
l(EF)2 = l(ED)2 + l(DF)2
⇒ (17)2 = (x)2 + (8)2
⇒ 289 = x2 + 64
⇒ x2 = 289 − 64
⇒ x2 = 225
⇒ `root 225`
⇒ x = 15
∴ The value of x is 15.
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
