Advertisements
Advertisements
Question
In the figure below, find the value of 'x'.

Solution
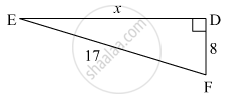
In the right-angled triangle EDF,
∠D = 90°.
Hence, side EF is the hypotenuse.
According to Pythagoras' theorem,
l(EF)2 = l(ED)2 + l(DF)2
⇒ (17)2 = (x)2 + (8)2
⇒ 289 = x2 + 64
⇒ x2 = 289 − 64
⇒ x2 = 225
⇒ `root 225`
⇒ x = 15
∴ The value of x is 15.
RELATED QUESTIONS
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
