Advertisements
Advertisements
Question
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
Solution
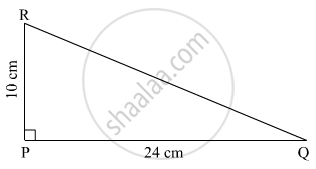
In the right-angled triangle PQR, ∠P = 90°. Hence, side QR is the hypotenuse.
According to Pythagoras' theorem,
l(QR)2 = l(PQ)2 + l(PR)2
⇒ l(QR)2 = (24)2 + (10)2
⇒ l(QR)2 = 576 + 100
⇒ l(QR)2 = 676
⇒ l(QR)2 = (26)2
⇒ l(QR) = 26
∴ Length of seg QR = 26 cm.
RELATED QUESTIONS
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
