Advertisements
Advertisements
Question
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution
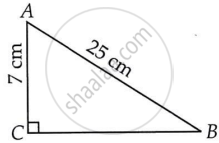
By applying Pythagoras theorem in ΔABC,
(AC)2 + (BC)2 = (AB)2
(BC)2 = (AB)2 − (AC)2
(BC)2 = (25)2 − (7)2
(BC)2 = 625 − 49
(BC)2 = 576
∴ BC = 24 cm
APPEARS IN
RELATED QUESTIONS
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
