Advertisements
Advertisements
Question
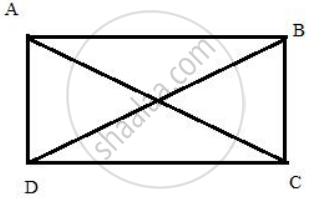
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Solution
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since, ABCD is a rectangle angles A, B, C and D are rt. angles.
First, we consider the ΔACD, and applying Pythagoras theorem we get,
AC2 = DA2 + CD2 ....(i)
Similarly, we get from rt. angle triangle BDC we get,
BD2 = BC2 + CD2
= BC2 + AB2 ....[ In a rectangle, opposite sides are equal, ∴ CD = AB ] ...(ii)
Adding (i) and (ii)
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
Hence proved.
APPEARS IN
RELATED QUESTIONS
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.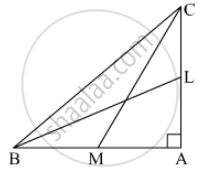
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
Use the information given in the figure to find the length AD.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
