Advertisements
Advertisements
Question
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
Solution
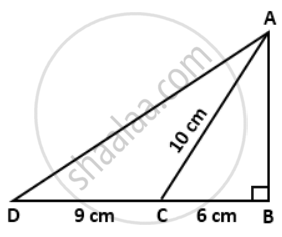
In ΔABC, ∠B = 90°
∴ AC2 = AB2 + BC2 ....(Pythagoras Theorem)
⇒ 102 = AB2 + 62
⇒ AB2 = 102 - 62
= 100 - 36
= 64
Now,
BD = BC + CD
= 6 + 9
= 15cm
⇒ BD2 = 225
In ΔABD, ∠B = 90°
∴ AD2 = AB2 + BD2
⇒ AD2 = 64 + 225 = 289
⇒ AD = 17cm.
APPEARS IN
RELATED QUESTIONS
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
The longest side of a right angled triangle is called its ______.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
