Advertisements
Advertisements
Question
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
Solution
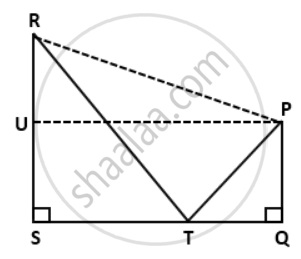
PQ = `"RS"/(3)` = 8cm
⇒ PQ = 8cm and RS = 3 x 8 = 24cm
3ST = 4QT = 48cm
⇒ ST = `(48)/(3) = 16"cm" and "QT" = (48)/(4)` = 12cm
In ΔPTQ,
PT2 = PQ2 + QT2
= 82 + 122
= 64 + 144
= 208
In ΔRTS,
RT2 = RS2 + ST2
= 242 + 162
= 576 + 256
= 832
Now, PT2 + RT2
= 208 + 832
= 1040 .....(i)
Draw PU ⊥ RS and Join PR.
PU = SQ
= ST + TQ
= 16 + 12
= 28cm
RU = RS - US
= RS - PQ
= 24 - 8
= 16cm
In ΔRUP,
PR2 = RU2 + PU2
= 162 + 282
= 256 + 784
= 1040 ....(ii)
From (i) and (ii), we get
PT2 + RT2 = PR2
Thus, ∠RTP = 90°.
APPEARS IN
RELATED QUESTIONS
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
Two angles are said to be ______, if they have equal measures.
In a triangle, sum of squares of two sides is equal to the square of the third side.
