Advertisements
Advertisements
Question
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD
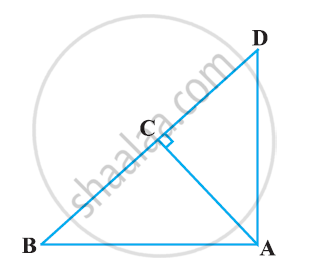
Solution
In ΔADB and ΔCAB, we have
∠DAB = ∠ACB (Each equals to 90°)
∠ABD = ∠CBA (Common angle)
∴ ΔADB ~ ΔCAB [AA similarity criterion]
`⇒(AB)/(CB) = (BD)/(AB)`
⇒ AB2 = CB × BD
APPEARS IN
RELATED QUESTIONS
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
