Advertisements
Advertisements
Question
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Solution
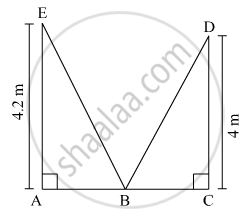
Let the length of the ladder be 5.8 m.
According to Pythagoras theorem,
In ΔEAB,
EA2 + AB2 = EB2
∴ (4.2)2 + AB2 = (5.8)2
∴ 17.64 + AB2 = 33.64
∴ AB2 = 33.64 − 17.64
∴ AB2 = 16
∴ AB = 4 m
In ∆DCB,
DC2 + CB2 = DB2
∴ (4)2 + CB2 = (5.8)2
∴ 16 + CB2 = 33.64
∴ CB2 = 33.64 − 16
∴ CB2 = 17.64
∴ CB = 4.2 m
From (1) and (2), we get
AB + BC = 4 + 4.2 = 8.2 m
∴ the width of the street is 8.2 m.
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In the figure below, find the value of 'x'.

Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Two squares having same perimeter are congruent.
Two circles having same circumference are congruent.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
