Advertisements
Advertisements
प्रश्न
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
उत्तर
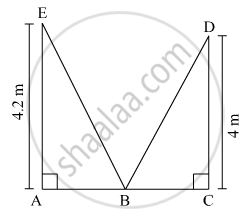
Let the length of the ladder be 5.8 m.
According to Pythagoras theorem,
In ΔEAB,
EA2 + AB2 = EB2
∴ (4.2)2 + AB2 = (5.8)2
∴ 17.64 + AB2 = 33.64
∴ AB2 = 33.64 − 17.64
∴ AB2 = 16
∴ AB = 4 m
In ∆DCB,
DC2 + CB2 = DB2
∴ (4)2 + CB2 = (5.8)2
∴ 16 + CB2 = 33.64
∴ CB2 = 33.64 − 16
∴ CB2 = 17.64
∴ CB = 4.2 m
From (1) and (2), we get
AB + BC = 4 + 4.2 = 8.2 m
∴ the width of the street is 8.2 m.
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Two rectangles are congruent, if they have same ______ and ______.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
