Advertisements
Advertisements
प्रश्न
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
उत्तर
Given, height of a pole is 8 m.
Distance between the bottom of the pole and a point on the ground is 6 m.
On the basis of given information, we can draw the following figure:
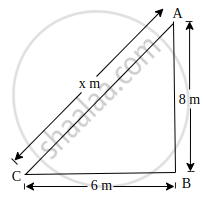
Let the length of the rope be x m
∵ AB = Height of the pole
BC = Distance between the bottom of the pole and a point on the ground, where the rope was tied . To find the length of the rope, we will use Pythagoras theorem, in right-angled ΔABC
∴ (AC)2 = (AB)2 + (BC)2
⇒ (x)2 = (8)2 + (6)2
⇒ x2 = 64 + 36
⇒ x2 = 100
⇒ x = `sqrt(100)` = 10 m
Hence, the length of the rope is 10 m.
APPEARS IN
संबंधित प्रश्न
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
