Advertisements
Advertisements
प्रश्न
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Advertisements
उत्तर
Given, height of a pole is 8 m.
Distance between the bottom of the pole and a point on the ground is 6 m.
On the basis of given information, we can draw the following figure:
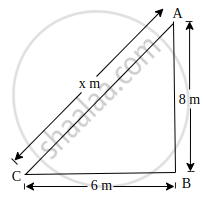
Let the length of the rope be x m
∵ AB = Height of the pole
BC = Distance between the bottom of the pole and a point on the ground, where the rope was tied .
To find the length of the rope, we will use Pythagoras theorem, in right-angled ΔABC
∴ (AC)2 = (AB)2 + (BC)2
⇒ (x)2 = (8)2 + (6)2
⇒ x2 = 64 + 36
⇒ x2 = 100
⇒ x = `sqrt(100)` = 10 m
Hence, the length of the rope is 10 m.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
